This week we looked at how to determine if what you think you’re seeing in your data is actually there. It was a warp speed introduction to a big chunk of what humanity now knows about truth-finding methods. Most of the ideas behind the methods are centuries or sometimes millennia old, but they were very much fleshed out in the 20th century, and these profound ideas haven’t percolated through to all disciplines yet.
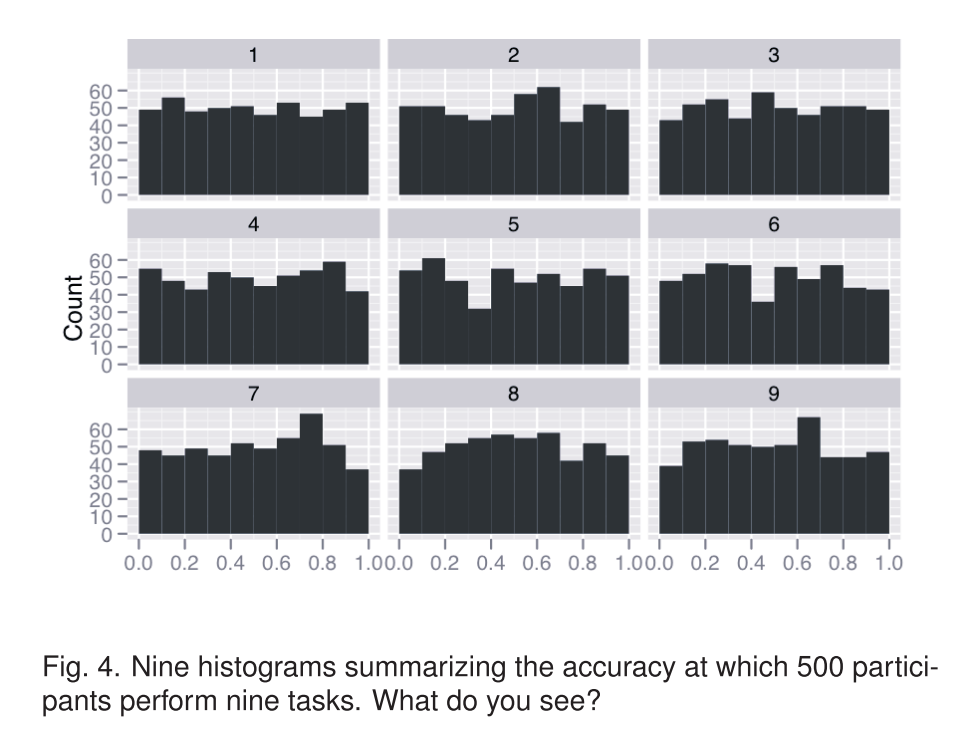
“Figuring out what is true from what we can see” is called inference, and begins with a strong feel for how probability works, and what randomness looks like. Take a look at this picture (from the paper Graphical Inference for Infovis), which shows how well 500 students did on each of nine questions, each of which is scored from 0-100% correct.
Is there a pattern here? It looks like the answers on question 7 cluster around 75% and then drop off sharply, while the answers for question 6 show a bimodal distribution — students either got it or they didn’t.
Except that this is actually completely random synthetic data, drawn from a uniform distribution (equal chance of every score.) It’s very easy to make up narratives and see patterns that aren’t there — a human tendency called apohenia. To avoid fooling yourself, the first step is to get a feel for what randomness actually looks like. It tends to have a lot more structure, purely by chance, than most people imagine.
Here’s a real world example from the same paper. Suppose you’re interested to know if the pollution from the Texas oil industry causes cancer. Your hypothesis is that if refineries or drilling release carcinogens, you’ll see higher cancer rates around specific areas. Here’s a plot of the cancer rates for each county (darker is more cancer.) One of these plots is real data, the rest are randomly generated by switching the counties around. (click for larger.)
Can you tell which one is the real data? If you can’t tell the real data from the random data, well then, you don’t have any evidence that there is a pattern to the cancer rates.
In fact, if you show these pictures to people (look at the big version), they will stare at them for a minute or two, and then most folks will pick out plot #3 as the real data, and it is. This is evidence (but not proof) that there is a pattern there that isn’t random — because it looked different enough from the random patterns that you could tell which plot was real.
This is an example of a statistical test. Such tests are more typically done by calculating the odds that what you see has happened by chance, but this is a purely visual way to accomplish the same thing (and you can use this technique yourself on your own visualizations; see the the paper for the details.)
It’s part of the job of the journalist to understand the odds. In 1976, there was a huge flu vaccination program in the U.S. In early October, 14 elderly people died shortly after receiving the vaccine, three of them in one day. The New York Times wrote in an editorial,
It is conceivable that the 14 elderly people who are reported to have died soon after receiving the vaccination died of other causes. Government officials in charge of the program claim that it is all a coincidence, and point out that old people drop dead every day. The American people have even become familiar with a new statistic: Among every 100,000 people 65 to 75 years old, there will be nine or ten deaths in every 24-‐hour period under most normal circumstances.
Even using the official statistic, it is disconcerting that three elderly people in one clinic in Pittsburgh, all vaccinated within the same hour, should die within a few hours thereafter. This tragedy could occur by chance, but the fact remains that it is extremely improbable that such a group of deaths should take place in such a peculiar cluster by pure coincidence.
Except that it’s not actually extremely improbable. Nate Silver addresses this issue in his book by explicitly calculating the odds:
Assuming that about 40 percent of elderly Americans were vaccinated within the first 11 days of the program, then about 9 million people aged 65 and older would have received the vaccine in early October 1976. Assuming that there were 5,000 clinics nationwide, this would have been 164 vaccinations per clinic per day. A person aged 65 or older has about a 1-‐in-‐7,000 chance of dying on any particular day; the odds of at least three such people dying on the same day from among a group of 164 patients are indeed very long, about 480,000 to one against. However, under our assumptions, there were 55,000 opportunities for this “extremely improbable” event to occur— 5,000 clinics, multiplied by 11 days. The odds of this coincidence occurring somewhere in America, therefore, were much shorter —only about 8 to 1
Silver is pointing out that the editorial falls prey to what might be called the “lottery fallacy.” It’s vanishingly unlikely that any particular person will win the lottery next week. But it’s nearly certain that someone will win. If there are very many opportunities for a coincidence to happen, and you don’t care which coincidence happens, then you’re going to see a lot of coincidences. You can see this effect numerically with even the rough estimation of the odds that Silver has done here.
Another place where probabilities are often misunderstood is polling. During the election I saw a report that Romney had pulled ahead of Obama in Florida, 49% to 47% with a 5.5% margin of error. I argued at the time that this wasn’t actually a story, because it was just too likely that Obama was actually still leading and the error in the poll was just that, error. In class we worked the numbers on this example and concluded that there was a 36% chance — so, 1 in 3 odds — that Obama was actually ahead (full writeup here.)
In fact, 5.5% is an unusually high error for a poll, so this particular poll was less informative than many. But until you actually run the numbers on poll errors a few times, you may not have a gut feel for when a poll result is definitive and when it’s very likely to be just noise. As a rough guide, a difference between two numbers of twice the margin of error is almost certain to indicate that the lead is real.
If you’re a journalist writing about the likelihood or unlikelihood of some event, I would argue that it is your job to get a numerical handle on the actual odds. It’s simply too easy to deceive yourself (and others!)
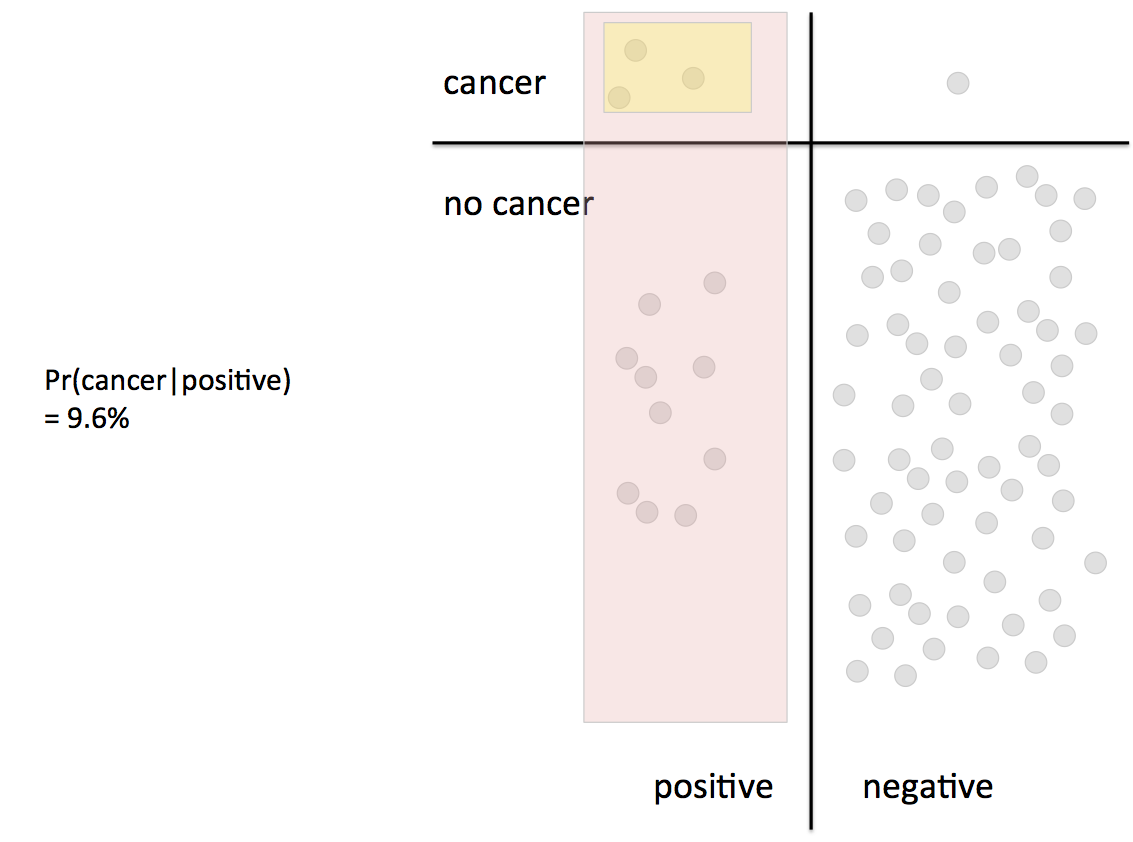
Next we looked at conditional probability — the probability that something happens given that something else has already happened. Conditional probabilities are important because they can be used to connect causally related events, but humans aren’t very good at thinking about them intuitively. The classic example of this is the very common base rate fallacy. It can lead you to vastly over-estimate the likelihood that someone has cancer when a mammogram is positive, or that they’re a terrorist if they appear on a watch list.
The correct way to handle conditional probabilities is with Bayes’ Theorem, which is easy to derive from the basic laws of probability. Perhaps the real value of Bayes’ theorem for this kind of problem is that it forces you to remember all of the information you need to come up with the correct answer. For example, if you’re trying to figure out P(cancer | positive mammogram) you really must first know the base rate of cancer in the general population, P(cancer). In this case it is very low because the example is about women under 50, where breast cancer is quite rare to begin with — but if you don’t know that you won’t realize that the small chance of false positives combined with the huge number of people who don’t have cancer will swamp the true positives with false positives.
Then we switched gears from all of this statistical math and talked about how humans come to conclusions. The answer is, badly if you’re not paying attention. You can’t just review all the information you have on a story, think about it carefully, and come to the right conclusion. Our minds are simply not built this way. Starting in the 1970s an amazing series of cognitive psychology experiments revealed a set of standard human cognitive biases, unconscious errors that most people make in reasoning. There are lots of these that are applicable journalism.
The issue here is not that the journalist isn’t impartial, or acting fairly, or trying in good faith to get to the truth. Those are potential problems too, but this is a different issue: our minds don’t work perfectly, and in fact they fall short in predictable ways. While it’s true that people will see what they want to see, confirmation bias is mostly something else: you will see what you expect to see.
The fullest discussion of these startling cognitive biases — and also, conversely, how often our intuitive machinery works beautifully — is the book by one of the original researchers, Daniel Kahneman’s Thinking Fast and Slow. I also know of one paper which talks about how cognitive biases apply to journalism.
So how does an honest journalist deal with these? We looked at the method of competing hypotheses, as described by Heuer. The core idea is ancient, and a core principle of science too, but it bears repetition in modern terms. Instead of coming up with a hypothesis (“maybe there is a cluster of cancer cases due to the oil refinery”) and going looking for information that confirms it, come up with lots of hypothesis, as many as you can think of that explain what you’ve seen so far. Typically, one of these will be “what we’re seeing happened by chance,” often known as the null hypothesis. But there might be many others, such as “this cluster of cancer is due to more ultraviolet radiation at the higher altitude in this part of the country” or many other things. It’s important to be creative in the hypothesis generation step: if you can’t imagine it, you can’t discover that it’s the truth.
Then, you need to go look for discriminating evidence. Don’t go looking for evidence that confirms a particular hypothesis, because that’s not very useful; with the massive amount of information in the world, plus sheer randomness, you can probably always find some data or information to confirm any hypothesis. Instead you want to figure out what sort of information would tell you that one hypothesis is more likely than another. Information that straight out contradicts a hypothesis (falsifies it) is great, but anything that supports one hypothesis more than the others is helpful.
This method of comparing the evidence for different hypothesis has a quantitative equivalent. It’s Bayes’ theorem again, but interpreted a little differently. This time the formula expresses a relationship between your confidence or degree of belief in a hypothesis, P(H), the likelihood of seeing any particular evidence if the hypothesis is true, P(E|H), and the likelihood of seeing any particular piece of evidence whether or not the hypothesis is true, P(E)
To take a concrete example, suppose the hypothesis H is that Alice has a cold, and the evidence E is that you saw her coughing today. But of course that’s not conclusive, so we want to know the probability that she really does have a cold (and isn’t coughing for some other reason.) Bayes’ theorem tells us what we need to compute P(H|E) or rather P(cold|coughing)
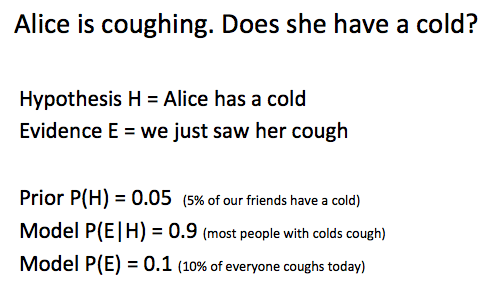
Under these assumptions, P(H|E) = P(E|H)P(H)/P(E) = 0.9 * 0.05 / 0.1 = 0.45, so there’s a 45% chance she has a cold. If you believe your initial estimates of all the probabilities here, then you should believe that there’s a 45% chance she has a cold.
But these are rough numbers. If we start with different estimates we get different answers. If we believe that only 2% of our friends have a cold at any moment then P(H) = 0.02 and P(H|E) = 18%. There is no magic to Bayesian inference; it can seem very precise but it all depends on the accuracy of your models, your picture of how the world works. In fact, examining the fit between models and reality is one of the main goals of modern statistics.
There’s probably no need to apply Bayes’ theorem explicitly to every hypothesis you have about your story. Heuer gives a much simpler table-based method that just lists supporting and disproving evidence for each hypothesis. Really the point is just to make you think comparatively about multiple hypothesis, and consider more scenarios and more discriminating evidence than you would otherwise. And not be so excited about confirmatory evidence.
However, there are situations where your hypotheses and data are sufficiently quantitative that Bayesian inference can be applied directly — such as election prediction. Here’s a primer on quantitative bayesian inference between multiple hypotheses. A vast chunk of modern statistics — most of it? — is built on top of Bayes’ theorem, so this is powerful stuff.
Our final topic was causality. What does it even mean to say that A causes B? This question is deeper than it seems, and a precise definition becomes critical when we’re doing inference from data. Often the problem that we face is that we see a pattern, a relationship between two things — say, dropping out of school and making less money in your life — and we want to know if one causes the other. Such relationships are called correlations, and probably everyone has heard by now that correlation is not causation.
In fact if we see a correlation between two different variables X and Y there are only a few real possibilities. Either X causes Y, or Y causes X, or Z causes both X and Y, or it’s just random fluke.

Our job as journalists is to figure out which one of these cases we are seeing. You might consider them alternate hypotheses that we have to differentiate between.
But if you’re serious about determining causation, what you actually want is an experiment: change X and see if Y changes. If changing X changes Y then we can definitely say that X causes Y (though of course it may not be the only cause, and Y could cause X too!) This is the formal definition of causation as embodied in the causal calculus. In certain rare cases you can prove cause without doing an experiment, and the causal calculus tells you when you can get away with this.
Finally, we discussed a real world example. Consider the NYPD stop and frisk data, which gives the date and location of each of the 600,000 stops that officers make on the street every year. You can plot these on a map. Let’s say that we get a list of mosque addresses, and discover that we discover that there are 15% more stops than average within 100 meters of New York City’s mosques. Given the NYPD history of spying on muslims, do we conclude that the police are targeting mosque-goers?
Let’s call that H1. How many other hypothesis can you imagine that will also explain this fact? (We came up with eight in class.) What kind of information or data or tests would you need to do to decide which hypothesis is the strongest?
The readings for this week were:
- The Psychology of Intelligence Analysis, chapters 1,2,3 and 8. Richards J. Heuer
- Correlation and causation, Business Insider
- If correlation doesn’t imply causation, then what does?, Michael Nielsen
- Graphical Inference for Infovis, Hadley Wickham et al.
- Why most published research findings are false, John P. A. Ioannidis